[Original draft 2024-11-15. After publishing my original series of posts analyzing the twins paradox, I realized I had more to say. This and the next post were written a few months later, but not published. A recent memory about an old textbook brought me back to this theme.]
I published a series of posts about the twins paradox and got bemused responses from those who looked at it. It is a popular puzzle among physics nerds, but most of us are not bothered by such impossible scenarios.
I did however, get a reply from someone who made an effort to resolve it with me, yet came up short. We both agreed that the paradox was broken by the situations not being symmetric (one twin experienced acceleration; the other did not). There was no paradox, yet there was still a puzzling discrepancy. Why would one twin’s path through spacetime result in a different time experience? What was the cause of it?
It didn’t seem to matter whether the acceleration (to change directions and return home) happened gradually or instantly; there was always a net proper-time difference. So the details of the acceleration didn’t seem to matter. Acceleration would not explain the time discrepancy.
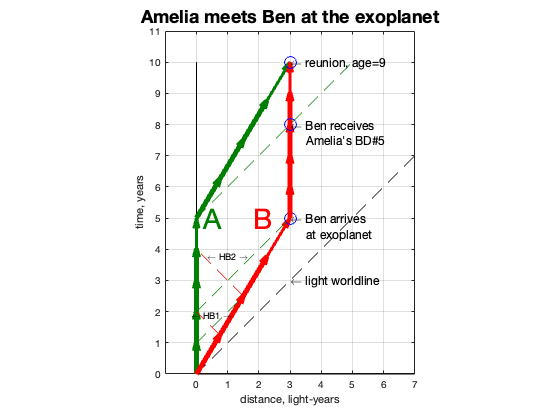
I considered some other scenarios. Here’s one I found amusing. Recall that the twins Amelia and Ben take different life paths: Amelia stays home while Ben travels to an exoplanet three light-years away, and then returns to find that Amelia has aged during his absence. But what if Ben stays on the exoplanet, and Amelia travels to join him there. Guess what? When they reunite, they are the same age!
I encountered a YouTube video that expressed this time dilation for young viewers as the result of traveling through spacetime at the speed of light. If you are traveling through space, then the forward motion through time is reduced. At the extreme, at the speed of light through space, the speed through time is zero.
Now the “traveling through space” part of this is subject to “who’s traveling?” It’s relative. When we do not experience acceleration forces, we are in an inertial frame. We do not know if we are traveling through space.
During the outbound trip by Ben, Amelia received his annual radioed happy birthday messages, but they arrived later than her birthday. She initially thought this was because Ben was traveling ever further away and the signals had to travel that distance (at lightspeed) back to her. But when she calculated the offset for time delay at Ben’s distance, there was a discrepancy.
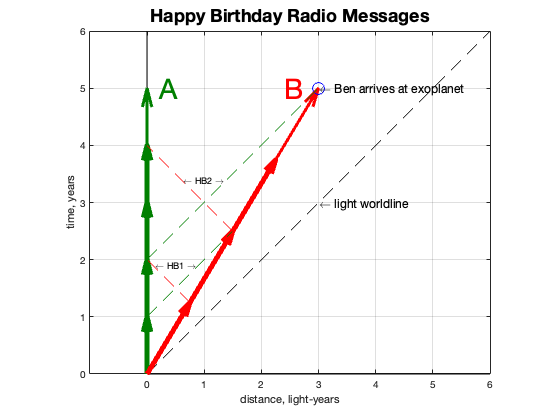
She received his one year birthday message after 2 years had elapsed. If he had sent the message one year after leaving Earth, he would be 0.6 light years away (Ben is traveling at 0.6c). At one year of travel, Amelia would figure that Ben’s message took 0.6 years to reach her, 1.6 years after he departed. She was expecting it at 1.6 years, yet it didn’t arrive until a full two years after! Did he really procrastinate for 0.4 years? What was going on?
Amelia got Ben’s birthday message after two years, but so did Ben! He would have made the same calculation: he is now 1.2 light years from home, so that is how long it took the message to reach him. But that means that Amelia must have sent it 1.2 years ago, only 0.8 years after they separated. Why would Amelia send a birthday message 0.2 years before her birthday?
This is the puzzle. And this is what the theory of relativity explains. Ben is traveling through space, so his travel through time is slowed. He is late on sending his birthday message because of that, not because he is further away from Earth. And because his time has slowed, he was only 0.8 years into his journey when Amelia sent her birthday message, but that is because his calendar was running slow.
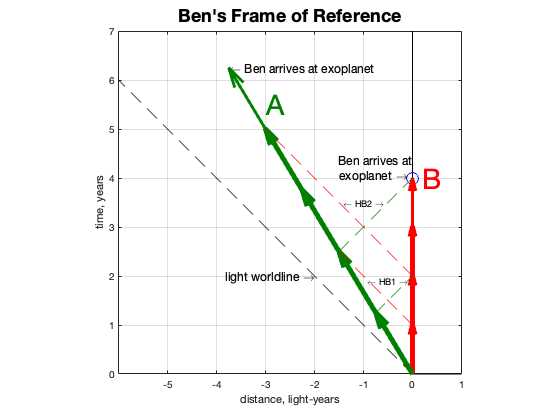
And it is all relative, because in Ben’s frame of reference, Amelia is moving through space (at 0.6c). When he receives Amelias first birthday message two years on, he assumes she is 0.6 light years away when she sent it and wonders why she sent it so late (by 0.4 years). Recall that Amelia had the same reaction.
So even after they exchange their first birthday messages, they each have reason to suspect something is mismatched in their experience of time.
When Ben arrives at the planet and stays there for a while, the rate of receiving messages from Amelia changes from one every two years to one every year. A year after arriving, as he is sending his HB#5, he receives Amelia’s HB#3. Since he is 3 light years away, Amelia must be six years older than when he left, while he is only five.
If Amelia stayed home, it would take a few more years before she started receiving messages annually. She would be sending HB#9 while receiving Ben’s HB#5 message. Adding the three-year transit time, she realizes that she is now a year older than Ben. They are in the same inertial frame, with the same delays on their messages.
If, instead, Amelia decided after five years to travel to the planet to visit Ben, she would undergo the same time dilation that Ben did on his trip. By the time she arrives, their age difference has vanished. This is now a symmetric experience between the twins, and there is no age difference to explain—no paradox.