A plan for 2017, but first, an introduction to celestial coordinates

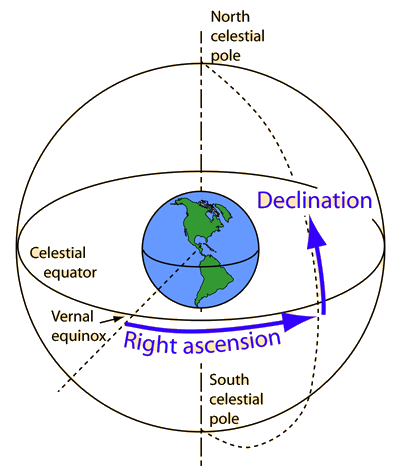
Astrometry is the term used for measuring the positions of the stars. It has a long history, dating from pre-telescope times, and which has introduced units that may seem archaic, but persist to this day (making them seem both arcane and archaic). Because of the Earth’s rotation, just like the sun, stars rise in the east and set in the west. The angular position in the sky depends on how many hours it has been ascending since “star-rise”.   If we pick one point in the sky as a reference, we can count the hours of ascension the star has traveled from that reference point: its “right ascension”. Right ascension (RA) is measured in hours, minutes and seconds, but is easily converted into its sky angle (24 hours equals 360 degrees).

I think of right ascension as the “horizontal” position in the sky (from east to west). The vertical coordinate, declination, is more conventional: it is the north-south angle from the Earth’s equator. These two numbers, right ascension and declination, define a star’s position in the sky.

Before photography, astrometry was conducted by aiming a fixed telescope at a specific declination angle, and the observer would watch the stars drifting through the field of view. When a target star appeared, the observer would mark the time at which it crossed the center of the view. This would be its right ascension, hence the units of time rather than angle.

When photographic emulsions became sensitive enough, the star field could be recorded and then the positions measured from the photographic plate. But because the Earth is rotating, the stars moved during the exposure, blurring their positions. This required that telescopes be equipped with “clock drives” so that they could track the star’s motion across the sky during the length of the exposure. This was the (mechanical, weight-powered) mechanism employed in Eddington’s expedition to track the sun and stars during his exposures, which lasted from 2 to 20 seconds.

As I contemplate the modern reconstruction of this experiment, I have the advantage of telescope mounts with motorized clock drives. I need only to align them with the Earth’s polar axis, and the battery-powered motors will do the rest. I also have the advantage of digital image sensors, but this comes with some tradeoffs as I hope to explain later.

The part of this experiment that will be challenging is to detect the background stars through the sun’s corona and any residual sky brightness. Eddington had the advantage of relatively bright stars, and a long, deep, period of totality. The stars we have available are at least 5 times dimmer, and totality will be two minutes, not six.

In anticipation, I have made plans to record the stars in the sun’s future gravitational neighborhood during the eclipse, and to compare them to the same field without the sun. There are two challenges. One is the practical ability to detect the starlight above the ambient light background of the sky and corona of the eclipse. The second is the technical ability to compare images taken before and during the eclipse, in order to measure the stellar deflections to subpixel accuracy.

I will outline the technical plan first, assuming that the stars will be successfully recorded on eclipse day. The issue of how to best detect them will follow.