I was able to obtain 35 photos during totality that were candidates to locate stars in the field. The exposures ranged from 1/60 to 2 seconds, but it became clear after applying the detection procedure starPos.m, that only the longest exposures, 1 and 2 seconds, would yield detected stars. The inner regions of the corona were just too bright and irregular for the algorithm to find them.
This left 15 images to work with. The camera orientation was good in that there were many candidate reference stars in the frame. Here is the mapping of a mid-eclipse exposure (3496):
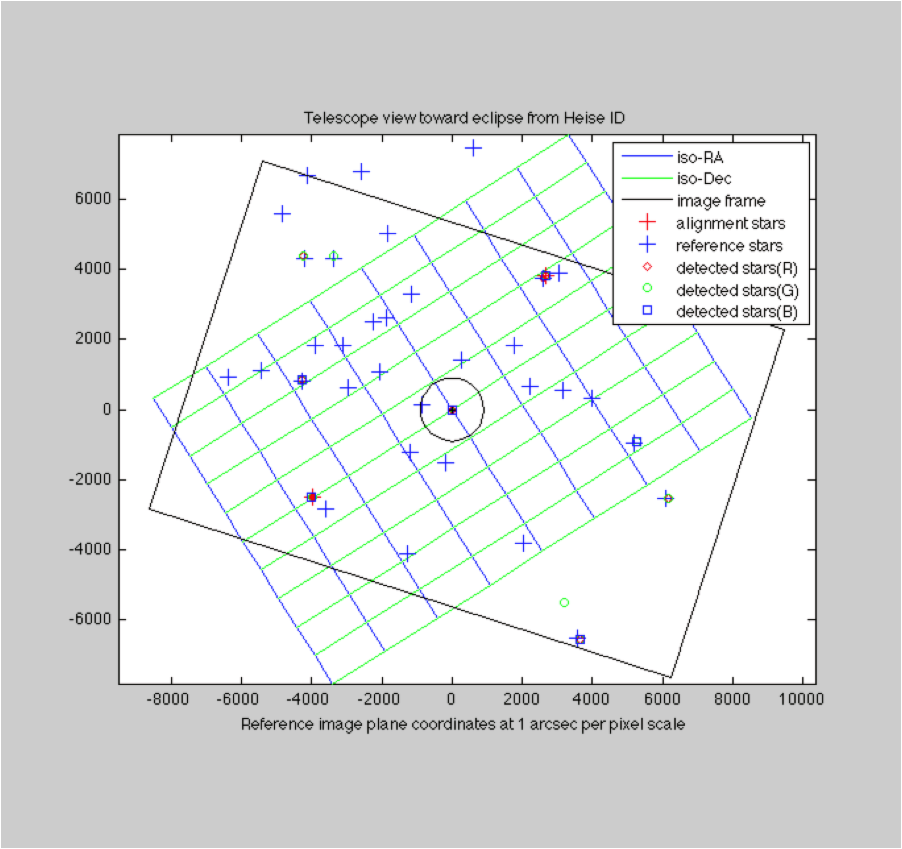
Here is a map of the located stars. The color codes indicate the channels (red, green or blue) in which the star was found. White indicates being found in all channels. The number of located stars for this image are: 6 red, 9 green, 5 blue.

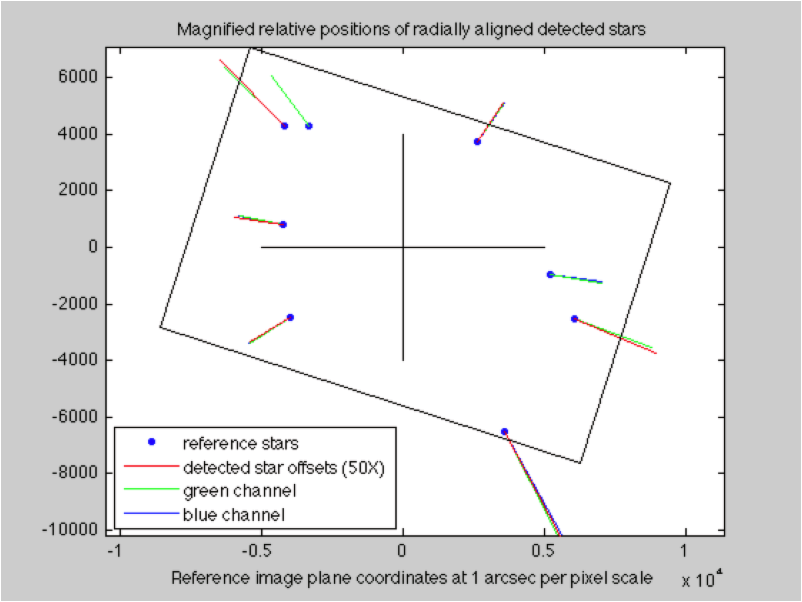
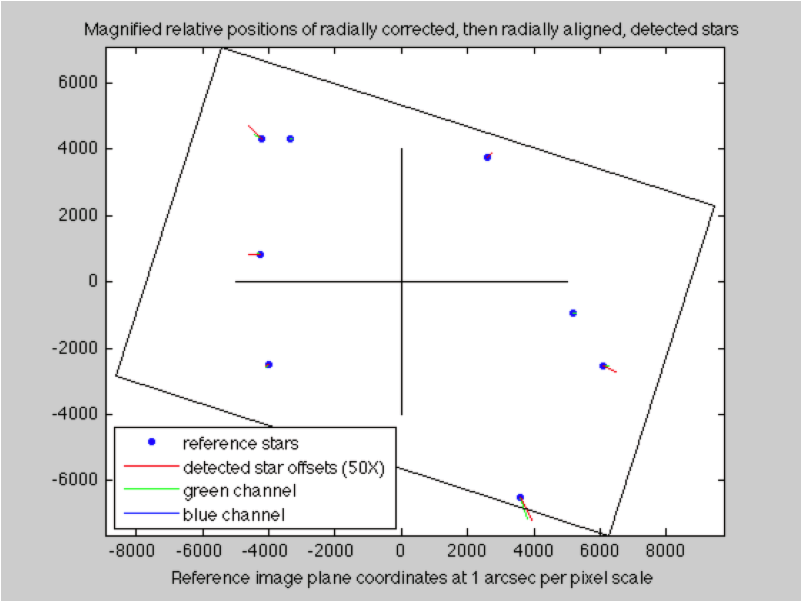
The detected stars are then mapped to our virtual camera view and correlated against our list of reference stars (imagePos.m). They are then more precisely aligned to the center of the sun. The lens distortion is removed at this stage (radialAlign.m).
The uncorrected lens positions look like this:
Lens corrected:
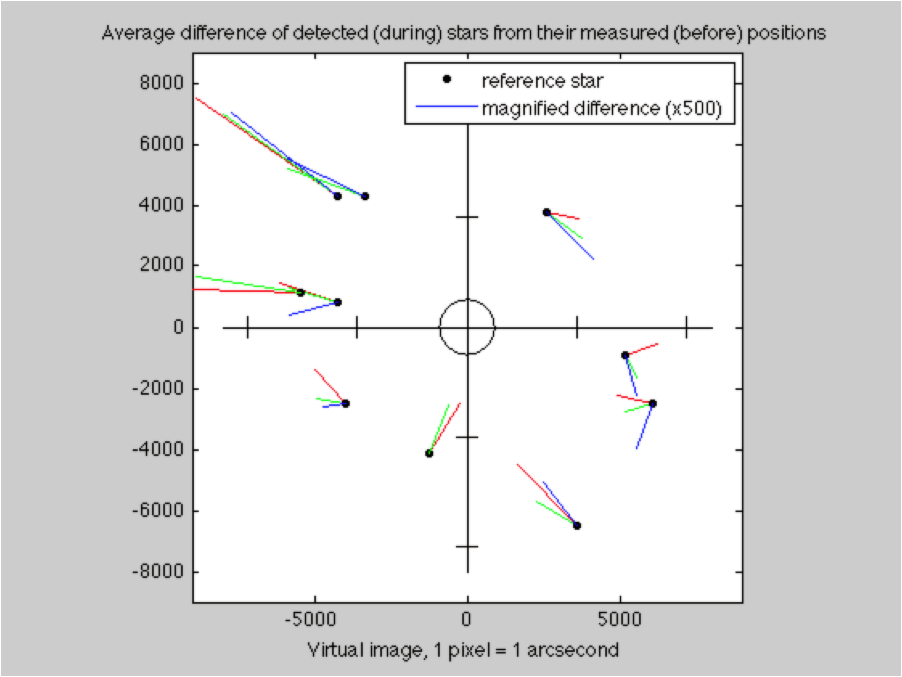
The errors are still rather large, but by collecting the statistics from all of the “during” frames, we can see how they land with respect to their published reference positions. The standard deviations are consistent with atmospheric seeing, but the differences in average positions indicates other sources of error.
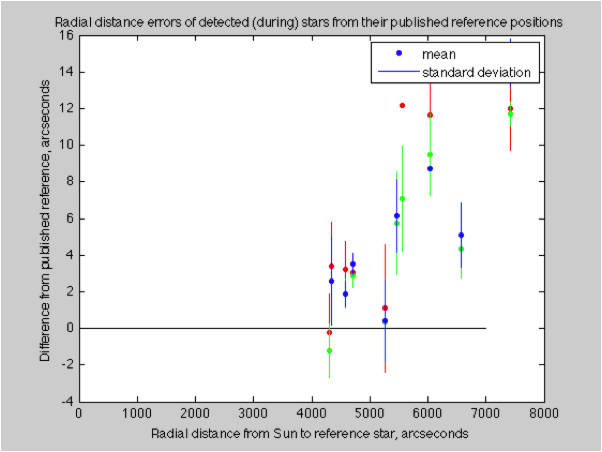
If we average all of the “before” images I took, and see how they compare to the published star locations, we get a similar wide ranging plot, the variances are again consistent with the seeing (but the average errors are not):
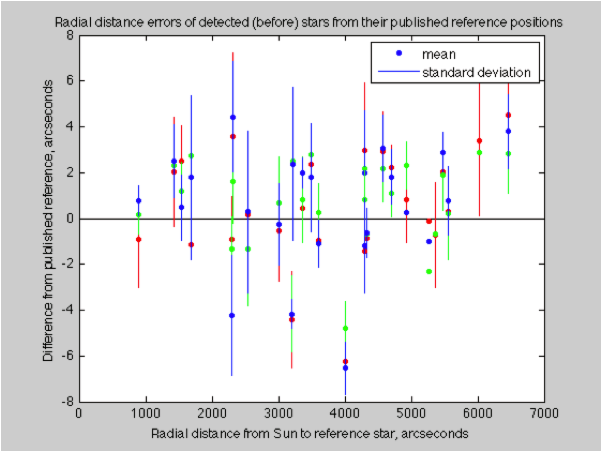
If we take the difference between these two data sets, we should see the gravitational deflection signal we are looking for. Unfortunately, it is lost in the noise.
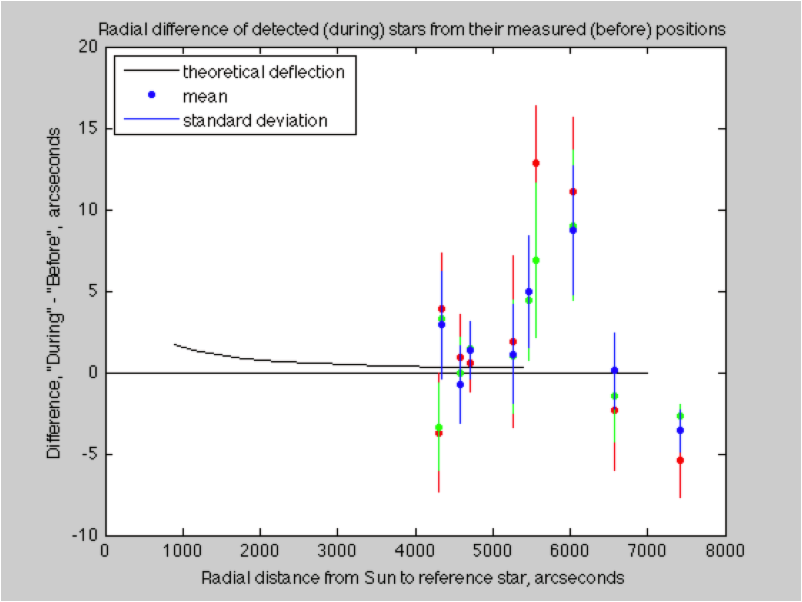
I can make a plot similar to Eddington’s that shows the average measured deflection of these reference stars, but I will not claim that it demonstrates gravitational deflection.