I think I can present this topic without math, but I will rely heavily on the visual tool of spacetime diagrams. Spacetime is the hybrid combination of space and time. It might sound abstract and scary, but it is really just recognizing that we travel in space and we travel in time. We can go anywhere in space, but we only go “forward” in time.
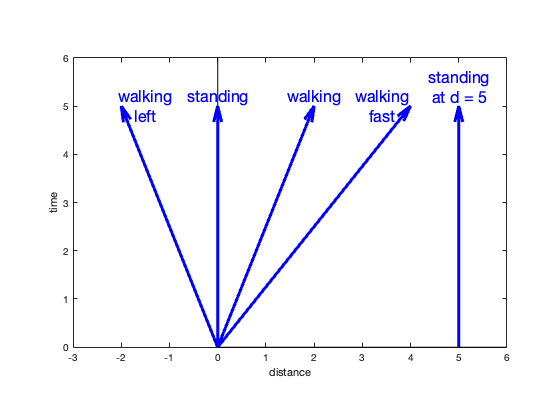
We can chart a path of our travels in spacetime on a graph where the x axis represents our relative position in space and the vertical axis is our position in time, labeled t. Yes, space is 3D, but the different directions in space can be folded into a single distance number.
If we stand still, we can plot our path in spacetime as a straight vertical line. Depending on where we are standing, the line will be somewhere on the distance axis. We can call our current position “zero”, and the line will fall on the time axis.
If we start walking to the right, the line will slant to the right as we move to further distances from our starting position. If we walk left, the line will slant left. If we walk faster, the lines will slant more. These plots are called “worldlines”.
When spacetime diagrams are used for plotting worldlines close to the speed of light, we use units of time and distance that match. Time is measured in the usual seconds, or maybe years, and distance is measured in units of how far light travels in a unit of time, so light-seconds (~30 million meters) or light-years (9.5 trillion kilometers). This choice of units results in a spacetime plot for light as falling on the 45-degree line. The speed of light is denoted by the letter c, which on the diagram is one light-year per year.
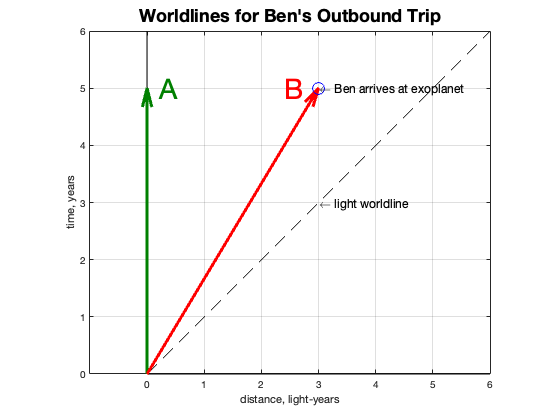
We can now depict Amelia and Ben’s worldlines. Let’s say that Ben departs at position 0, at time 0, at a velocity 60% the speed of light, 0.6c. Amelia (I will sometimes just call her “A”) follows the green worldline. Ben (“B”) charts a red path to the right with a slope that matches 0.6c—for every vertical unit of time, Ben moves to the right 0.6 units of distance. Five units of time results in covering 3 units of distance. Since the exoplanet is 3 light years away, it will take five years to reach it. Here is a plot with units of years and light-years.
Special relativity is based on a rather unusual premise: that the speed of light is measured to be the same in all inertial frames of reference, no matter their velocity.
A consequence of this premise is that each tick of a moving clock takes longer, at least as seen by a non-moving observer. The moving observer doesn’t notice his clock ticking more slowly, but when he looks back at a non-moving clock, it appears to be the slow one.
The clock in your own inertial frame of reference tells you the “proper time”. Every observer experiences it as the normal passage of time. There is no clue that it appears slower to other reference frames. This effect of the apparent slowing of moving clocks is called “time dilation”.
Units of proper time can be depicted on the spacetime diagram by short vectors that represent one unit of time as experienced by the observer in its frame. Amelia’s units of proper time are shown as head to tail arrows along her worldline on the vertical axis. Ben’s are head to tail arrows along his worldline.
Ben’s proper time unit being longer than Amelia’s is a result of the premise: the speed of light is the same in all reference frames. As you get closer to the speed of light, in order to measure its velocity (distance per unit time) as the same, either the time units have to get larger, or the distance units have to get smaller, or both (which is what actually happens, but we are focusing on time dilation here). The lengthening of the time step is prescribed by the mathematics of relativity so that the speed of light looks the same to everyone, moving or not.
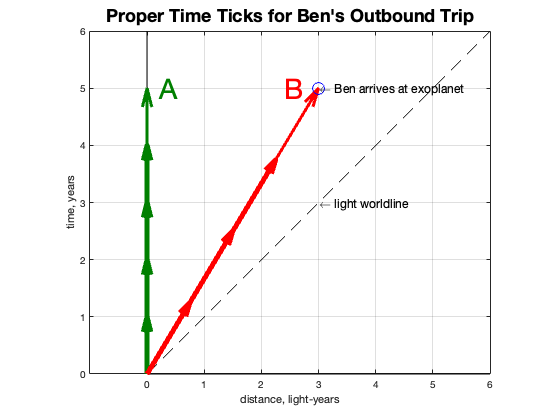
So now we have time units for each frame. Each tick of the clock moves the person on their worldline in the time direction; Amelia’s is straight up because she is staying put, and Ben’s tick is tilted up and over because he is moving in both time and position. The length of Ben’s tick has been increased to make his speed of light measurement be correct.
We can imagine that Amelia and Ben made arrangements to send happy birthday messages to each other on their common birthday, radio transmissions inserted into the telemetry stream between the spaceship and Earth. We can also imagine that they had a blast when Ben departed on their birthday.
Radio signals travel at the speed of light and so the worldlines of those transmissions fall on 45-degree diagonals. We can plot the first few of them and see what the twins experienced.
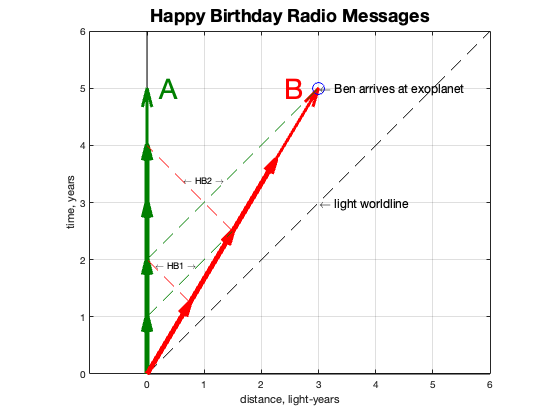
Amelia sends her first happy birthday message, HB1, one year after Ben departed. She recognized that Ben was now 0.6 light years away, and since the message had so far to travel, she didn’t expect anything from him until later that year, maybe 7 months or so.
But notice that Ben’s year is a little longer than Amelia’s, so his happy birthday message is sent “late” (even though he thinks he is exactly on time). At the time Ben sends the message, another 3 months has gone by for Amelia. And if he has been traveling for a year and 3 months, he is now more than 0.6 light years away; he is 0.75 light years distant. And from that distance it takes 9 months for the message to make it to Amelia. That additional time, plus the 3 month delay in even sending it, results in a full year before Amelia gets it. As Amelia is sending her second happy birthday message, she finally receives HB1 from Ben!
Ben also doesn’t expect to hear from Amelia each year. He knows he is traveling farther away and the signal needs additional time to reach him. And in fact, it takes two years (on B’s calendar) to receive the first message from A.
I once thought that time dilation was entirely due to the increasing distance and how long it took for the signals to get back. But it is more. B’s clock is running slow, so Ben doesn’t even send his message until three months after Amelia’s birthday. And since it was sent late because of the slowed clock, the message took longer to get back because the ship was farther away when he sent it.
This pattern continues for the rest of the trip to the exoplanet. When he lands, Ben has sent 4 birthday messages, Amelia has sent 5. B has received two of A’s five messages, and A has received 2 of B’s four.
So far we have been showing the trip from Amelia’s perspective. It might be interesting to show how it looks from Ben’s. Relativity theory provides a way to convert back and forth between inertial frames of reference. It is called the Lorentz transform and it accounts for time dilation and length contraction while always keeping the speed of light constant. Here is the spacetime diagram for Ben’s outbound trip where he is considered the “observer at rest”.
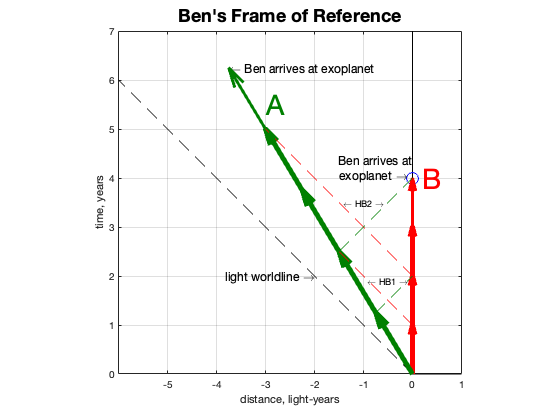
You can see that this is NOT a perfect reflection of Amelia’s perspective. She is moving left while Ben is standing still in his reference frame. Ben’s worldline runs for four years on his calendar, but Amelia’s runs for five of hers, which are longer than Ben’s, since to him, she has the moving clock. The messages they send each other arrive at the same interval in each frame, every two years, just as before. At the time Ben reaches the exoplanet, they have each received two messages.
So far there is no paradox, but Amelia and Ben have not been reunited yet, so there is no way to directly compare their relative ages.

Pingback: The Twins Paradox – Introduction | Spontaneous Emissions
Pingback: The Twins Reunite | Spontaneous Emissions
Pingback: The Twins Paradox – a lifelong puzzle | Thor's Life-Notes