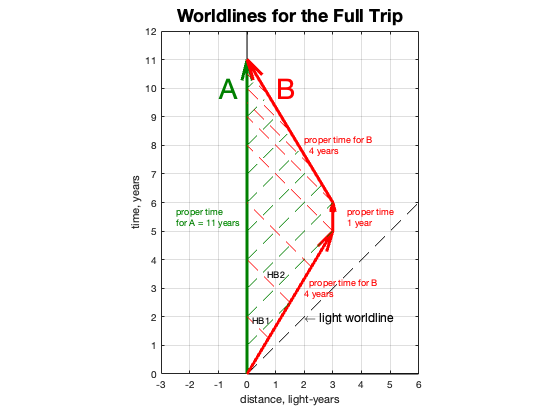
At this point, Ben stops to take his samples and make measurements and survey the exoplanet. He spends a year doing this, but he is no longer moving away from Amelia. Their clocks are each ticking at the same rate. Since they are three light years apart, it will take three years for B’s messages to be received by his twin.
After sending Happy Birthday message #5, Ben takes off for his return trip home. His spaceship is capable of traveling at 0.6c, so it will take 5 years to cover the 3 light year distance. But this is not what Ben experiences. On his calendar it only takes four!
Again, this is because at this speed the units of time for B are longer, so the clock ticks are slower in order for B to observe the speed of light in his proper time as c.
B continues to transmit the HB signals and A receives them. They are arriving delayed of course– B is still light years away, but they come more frequently now because each year B is closer and the signal transit time is shorter. It is not shorter by 0.6 years; it comes earlier than expected, 0.5 year. This is because Ben is still sending them every year on his birthday, but on his calendar, which is 1-1/4 years apart for Amelia. And in that extended time, he is even closer, so the remaining distance for the signal is shorter and takes less time, 0.5 instead of 0.6 years.
Ben finally arrives home and is now two years younger than Amelia. She has aged 5+1+5=11 years. Ben has aged 4+1+4=9 years. We have just seen how time dilation as a result of B moving close to the speed of light is the cause. His proper time along his world line is less than A’s proper time along hers.
This is not an intuitive result. It feels wrong somehow, but it is how the universe works. It has been confirmed over and over—moving clocks tick more slowly! In 1971 an experiment was run where atomic clocks were flown around the world and then compared to the reference clock on the ground. The differences were tiny but measurable– nanoseconds, and matched the theory.
But when we finally accept that this is how the universe works, we are still left with trying to explain the paradox. Why isn’t the viewpoint from Ben, where A rushes off, the exoplanet rushes in, and he remains stationary in his inertial spaceship frame, an equally valid representation?
And here is the answer—Ben is NOT in a purely inertial frame of reference. “Inertial frame of reference” means NO acceleration, no change in velocity or direction. Ben experienced both. Amelia didn’t.
An inertial frame of reference is a straight line on a spacetime diagram. While it is possible to use the Lorentz transformation to portray Ben as standing still for one of the legs of his journey, it is not possible to transform his full worldline into a single straight path. His path will always have some kink in it that takes him out of the inertial frame.
This is the crux of resolving the paradox. The two worldlines are NOT both inertial frames. There is an asymmetry in the problem. They are not equivalent. B experienced rapid deceleration followed by a change of direction and an acceleration, all of which are non-inertial conditions and not covered by the rules of special relativity.
Paradox resolved: the two perspectives are not physically equivalent, so it is not necessary that the proper times of the two paths match.

Pingback: Spacetime and Worldlines, Ben’s Outbound Trip | Spontaneous Emissions
Pingback: So is Acceleration Responsible? | Spontaneous Emissions
Pingback: Spacetime and Worldlines, Ben’s Outbound Trip - Spontaneous EmissionsSpontaneous Emissions