So is Acceleration Responsible?

The symmetry argument made in the twins paradox is now broken, but what is it about those non-inertial events that prevents us from considering the separate legs of space travel—away and back, as two independent segments of a single inertial worldline?  Something must be happening at that transition point.  Are the g-forces responsible for the time discrepancy?

This is what I thought after recognizing the asymmetry.  But it turns out this is a red herring.

The B worldline reaches the destination and then abruptly stops.  At 0.6c, Ben and the spaceship would be flattened in less than a microsecond.  Maybe all that time dilation would have been resolved, but Ben didn’t live to tell us about it.

Maybe if there was a more gradual deceleration, the time discrepancy could be explained.  Many YouTube videos point to the acceleration as the cause of the twins’ age differences.

I thought this for a while too, and I was ready to sweep it under the general relativity rug.

But after learning special relativity from eigenchris, I no longer believe that gravity and the warped spacetime of general relativity are necessary to explain it.

It is possible to measure time dilation during acceleration and deceleration without general relativity.  So I constructed a worldline for Ben that had him gently decelerating to land on a (different) exoplanet.  It added time to the overall mission, but kept him alive to complete it.

The deceleration created a force on Ben, but it was limited so that he felt the equivalent of Earth’s gravity-  1g.  It took almost 9 months (but he only thought it was 8) to slow down and stop at the exoplanet.

This time, B stops only long enough to collect some samples and blast off again, following a 1g acceleration curve until he reaches the 0.6c cruising speed of his spaceship, at which, like before, he spends 4 years of his proper time.

This time, when reunited, B is 4+1.3+4=9.3.  A is 5+1.4+5=11.4  Ben is now 2.1 years younger than Amelia, even more than before!  But then, his mission lasted longer so his clocks were in motion longer.

If we look more closely at the deceleration/acceleration segment, we find that the ratio of proper times, B/A is about 0.9 (Ben’s watch ticked 9 times on average to Amelia’s 10).  What if the acceleration had been more?  Or less?  I explored these possibilities and found that they would take less time (or more), but the ratio of proper times remained the same!

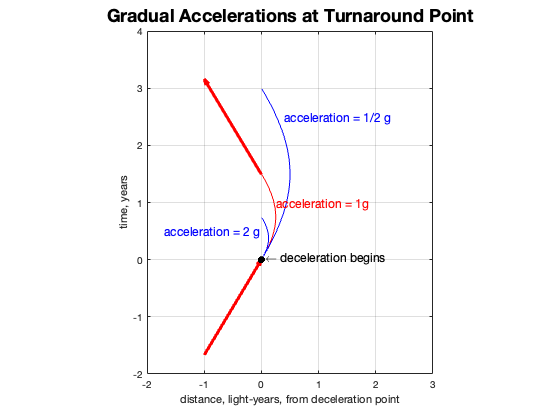
Decel/Accel rate	Total Distance, light years	Time, T years	Proper Time t  years	Ratio t/T
0.5g	1	2.958	2.727	0.922
1g	0.5	1.479	1.3636	0.922
2g	0.25	0.7395	0.6818	0.922
10g	0.05	0.1479	0.13636	0.922
100g	0.005	0.01479	0.013636	0.922

So no matter what acceleration you applied at the turnaround point, there is no recovering of the time discrepancy between the world paths of A and B.

Returning to the same position cannot be done without incurring an acceleration.  It is not possible for the twins to reunite without one or both of them exiting their inertial frame and feeling the forces of acceleration.  So in a way, acceleration is necessary for the twins to get back together and compare their elapsed proper times, but it is not the “cause” of the discrepancy.  Instead, it is the speed and duration of time spent in motion. 

This is what finally convinced me that time dilation was more than just the effects of remote signaling from a fast-moving object, and that there was no explanation to be found in its acceleration.  It was truly an effect of objects moving with respect to my local reference frame!

The twins paradox is puzzling because it is not our experience that our personal time is shifting when we move around.  It does– we just never notice it.  So it seems strange that biological aging can change by taking a high speed trip.  But is it really any more strange than the premise that the speed of light looks the same to everyone, no matter how fast they are going?  This is the actual source of the paradox.  If we can accept that, then we can accept that moving clocks tick more slowly!

Returning to Ben’s experience, I suspect there is more to understand about switching between different inertial frames.  That understanding can be found in general relativity theory but I will stop here, having now satisfied my lifelong mystery of the twins paradox.

This has been my attempt to explain it.  If it makes sense to you, let me know.

---

previous | intro | next